伟德体育(BetVictor Sports)国际官网第 3 章：从可靠的大数据来源到通过生态生理变量捕捉运动表现《体育表现分析中的人工智能

　　伟德体育(BetVictor Sports)国际官网(访问: hash.cyou 领取999USDT）技术进步为进一步研究和增进对运动表现的理解提供了机会，因为（i）它们提供了过去无法获得的数据，（ii）它们允许计算过去无法完成的指标（见第1章）。例如，机器学习和深度学习技术允许克服“低水平”指标的计算，增加“高水平”指标（例如，团队内部和团队之间的组织），这可以在比赛和/或训练期间完成。为了快速向从业者提供关于运动员行为和表现的反馈，技术进步开发了新的设备和新的应用/算法（例如，智能手表、智能手机、全球定位系统（GPS）等嵌入式传感器，通常辅以加速度计，构成惯性测量单元（IMU））以及新的跟踪系统，特别是基于计算机视觉的进展（例如，多摄像机运动捕捉、电视广播跟踪、深度学习方法用于3D无标记运动捕捉、RGB深度相机）。

　　技术进步带来的一个问题是，传感器总是会为科学家和从业者提供一些数据，即使这些数据收集得不好，不能很好地反映实践的核心，或者反映了一个脱离情境或不具代表性的数据收集协议，这证实了数据驱动方法的弱点（Couceiro等人，2016）。此外，第二个问题是数据过多，这要求科学家使用人工智能技术（例如，机器学习或深度学习）进行数据降维和维度缩减。这些问题引发了数据降维和数据建模如何不减少对从业者有意义的信息的问题。此外，在模糊数据、降低维度和建模数据时，结果对于教练来说有时难以理解和解释，因为从数据分析到运动干预的转换远非直接的。这些风险可以通过适当设计数据采集程序、定义评估任务、数据收集方法和相关技术来克服。

　　我们认为，适当设计的方法应该植根于生态动力学框架。这个框架的一个理论支柱是感知 - 行动耦合（Araújo & Davids 2015; Araújo, Davids, & Passos, 2007），并强调代表性（实验）任务设计的重要性（Brunswik, 1956）。Brunswik（1956）提出了代表性设计这一术语，以倡导在有机体 - 环境关系层面研究心理过程。这意味着情境变量应该从有机体的环境中采样，以代表有机体行为的环境，并且实验中的行为旨在推广到该环境。代表性设计的这一定义强调了确保学习、训练或实验任务约束代表表现或比赛/竞赛环境的任务约束的必要性，这是研究的特定焦点。代表性设计意味着强烈强调运动员与环境之间关系的特异性，这在行为科学的数据驱动方法中可能被忽视。执行者检测和利用环境信息以支持其行动的能力取决于感知和运动过程之间准确而有效的关系，称为感知 - 行动耦合（Pinder, Davids, Renshaw, & Araújo, 2011a）。

　　此外，这项研究还指出了在使用视频支持学习、训练和表现分析时需要谨慎，如果使用不当可能会使感知与行动脱节。在另一个例子中，Pinder, Davids, Renshaw, 和Araújo（2011b）强调了使用球投射机等设备的风险，因为它们可能会从表现环境中移除关键信息源（例如，投球手的运动），并显著影响板球击球中拦截动作的时机和控制。这些作者观察到练习任务约束之间存在显著差异，面对投球手时，后摆、前脚移动、下摆和前脚放置的起始时间更早，而面对投球机时则相反。因此，当面对投球手投球时（由感知和行动之间的功能耦合支持），可能会期望更具体的技能转移，而当投球机投球时可能会发生一般技能转移。当使用新技术进行干预和数据收集时，科学家和从业者必须意识到这种设备可能会对技能转移的特异性产生影响。当然，当使用投球机投球时，任务的可重复性很高，运动分析可以主要集中在击球手身上。

　　此外，数据收集技术和数据分析计算方法需要对从业者有意义。为了增强代表性设计，任务应该被视为：（i）复杂的和（ii）动态的，为学习者提供探索随时间演变的各种任务解决方案的机会；（iii）新颖的且与可实现的目标相关；（iv）支持主动感知；（v）提供对周围环境中关键信息源的充分访问（Davids, Araújo, Hristovski, Passos, & Chow, 2012）。考虑到这些方面，本章回顾了不同的数据收集设计方法，定义了任务、程序和相关技术，重点强调可靠性（两个系统之间的同质性或一致性；例如，测试 - 重测之间的稳定性或可重复性，如观察者间和观察者内的等效性）。当考虑可靠性时，可以评估准确性和精密度。准确性与测量值和部件实际值之间的差异有关，而精密度描述了用同一设备重复测量同一部件时的变化。最后，我们还研究不同技术设备的有效性（设备或捕捉系统测量其理论上预期测量的程度）。

　　Duthie, Pyne, 和Hooper（2003）分析了基于视频的时间 - 运动分析对十名橄榄球联盟球员的可靠性，这些球员在12场比赛中由一名观察者在两个不同时间（相隔一个月）进行单独评估。测试 - 重测可靠性被量化为测量的典型误差（TEM），并计算为重复分析之间差异分数的标准差除以（Hopkins, 2000），并评为好（）、中等（）或差（）（McInnes, Carlson, Jones, & McKenna, 1995）。在运动类别（步行、慢跑、大步走、冲刺、静态用力、静止）中花费的总时间具有中等至差的可靠性（TEM）。个体运动的频率具有好至差的可靠性（TEM），而个体运动的平均持续时间具有中等可靠性（TEM）。Duthie等人（2003）得出结论，基于视频的橄榄球运动员运动的时间 - 运动分析具有中等可靠性，不同运动类别可靠性存在差异，其中慢跑分析的可靠性最好，而静止和高强度活动（如大步走和冲刺）的分析可靠性较低。冲刺分析的较低可靠性可能归因于运动项目之间运动模式的差异，证实了观察者的经验可能会影响他们的评估。这项研究表明，个体观察者在进行时间 - 运动分析时应该量化他们的可靠性，特别是与其他系统（如全球定位系统（GPS）（Dogramac, Watsford, & Murphy, 2011）、惯性测量单元（IMU）（Dadashi等人，2013）或视频跟踪系统（Roberts等人，2006））相比。例如，Roberts等人（2006）使用一个五摄像机跟踪系统记录了橄榄球中七种活动（站立、步行、慢跑、中强度、高强度、最大强度跑步）的距离和跑步速度，并将该系统与符号分析进行了比较。观察者内和观察者间结果的可靠性使用测量的典型误差（TEM）进行测量。在20分钟内，平均行进距离为和，活动变化的平均次数为和，分别对应符号分析和数字化方法；平均速度在符号分析方法中具有平均绝对差异为。Roberts等人（2006）认为，使用七个项目对活动进行分类可能会增加符号分析中选择适当活动的难度。

　　此外，视频跟踪系统能够提供活动期间的减速/加速信息，而符号分析只提供平均速度。因此，数据分析的可靠性确实取决于任务设计和程序（例如，用于对活动进行分类的观察项目数量）。为了提高有效性和可靠性，观察者可以一起训练，就观察到的表现指标达成一致，进行盲观察（即，不知道其他观察者的结果），然后比较各自的分析，讨论观察结果之间的任何差距以理解和纠正错误来源，最后重复这个过程直到达到高水平的可靠性。在游泳中，Seifert等人（2006）比较了新手和专家观察者检测定义手臂划水阶段（即，入水、滑行、抓水、拉水、推水和恢复）关键 点的能力。均值（t检验）和方差（F检验）的组间比较揭示了在检测定义拉水阶段开始的抓水关键点上存在显著差异。进一步的调查表明，新手观察者需要50小时的训练才能提供可靠的观察。当观察者在观察特定事件方面具有较高的专业知识时，符号分析数据与3D运动学跟踪软件的数据之间没有显著差异（Seifert等人，2006）。当专家观察者的符号分析与从IMU（由3D加速度计和3D陀螺仪组成的惯性测量单元）计算的数据进行比较时，也获得了手臂划水阶段和协调指数的类似结果（Dadashi等人，2063）。

　　总体而言，RMSPE和CV值表明对各种指标的预测非常准确。一些分层指标，即速度和极高速距离，由于球员在这些状态下花费的时间较少，具有较大的CV值，但在这些情况下RMSPE仍然足够低，可以在实际环境中使用。特别是，速度的RMSPE仍然只有6.4秒；对于总距离，考虑到球员在每场比赛中平均行进3,524 m，RMSPE为183 m（Mortensen & Bornn, 2020）。总之，电视广播跟踪的当前技术水平很有前景，因为它使我们能够预测球员的活动；然而，它还没有被用于评估人际协调或团队集体行为的任何其他指标。它为改进在线比赛分析提供了优势。此外，人们可以认为类似的技术可以用于训练课程分析。然而，在实践中，摄像机设置可以更好地控制，以避免未被观察到的球员和空间遮挡。

　　当使用多视频相机系统时，包括不同的视角以及可能的广角镜头，必须参照校准平面（用于2D分析）或体积（用于3D分析）使用足够的校准点（如平面的网格或棋盘）来校正视差和失真（平移和旋转）。通过直接线性变换（DLT）（Abdel - Aziz & Karara, 1971）进行的坐标重建，在每个视野中使用更多的校准点时会得到改善（Brewin & Kerwin, 2003）。摄像机校准过程中的任何误差首先会在后续的数据处理中引入系统误差。另一个误差来源是数字化过程。实际上，解剖标志的简单手动数字化容易出错，并且数字化过程的操作者内和操作者间可靠性必须像之前符号分析中描述的那样进行计算。为了减少校准误差和数字化误差，建议使用足够的摄像机记录任务发生的体积，因为跟踪准确性取决于摄像机的数量。然而，大量的摄像机也会增加数字化过程的需求，特别是在手动或半自动跟踪的情况下。手动数字化总是非常耗时，是手动视频跟踪的一个主要问题（Mooney等人，2015; Wilson等人，1999）。

　　三维（3D）视动分析基于对关节上放置的反射标记的自动检测，目前是运动捕捉的金标准。这些系统需要使用多个摄像机，其设置、位置、分辨率和校准决定了一个用于分析运动的体积。环境光应该被控制，以保证对反射身体标记的良好跟踪，这使得视动相机系统更适合室内数据收集而不是室外。跟踪问题取决于被跟踪物体的数量、物体之间空间和时间遮挡的程度、摄像机的规格（例如，分辨率5 - 26 MP，帧率100 - 1,400 Hz，窄到广角镜头，最大捕捉距离10 - 40 m）、摄像机的数量以及物体被跟踪的捕捉距离和体积（Barris & Button, 2008; Pers, Bon, Kovacic, Sibila, & Dezman, 2002）。对于多视频相机系统，这个体积因此取决于用于测量的摄像机数量，这与时空记录的准确性成正比（de Jesus等人，2015）。然而，使用的摄像机越多，视动系统的成本就越高（Carse, Meadows, Bowers, & Rowe, 2013）。随着经济实惠的3D运动分析系统（例如，OptiTrack系统）的出现，这个财务限制得到了解决，这些系统提供了准确的解决方案来跟踪反射标记（Carse等人，2013; Thewlis, Bishop, Daniell, & Paul, 2013）。实际上，Thewlis等人（2013）发现在步态中Vicon系统和OptiTrack系统之间的绝对角度差异不超过。使用相同的系统，Carse等人（2013）在比较标记之间的距离时也发现记录的平均矢量大小（1 - 3 mm）有高度的一致性。尽管成本不再是使用3D视动系统的直接限制，但它们往往主要在实验室条件下使用（Ceccon等人，2013）。

　　因此，假设在高速（高于）和非直线跑步且方向急剧变化期间速度测量容易出错，从业者在将球员的活动分解为0到之间的速度区域时可能需要谨慎。当进行这样的划分时，由于性别、球员在场上的位置（进攻球员/防守球员）或年龄导致的高强度冲刺次数或在高速区域花费的时间的可能差异可能掩盖可靠性的不足。实际上，很少有研究将GPS的可靠性与金标准运动捕捉系统进行比较（Randers等人，2010；Waldron等人，2011）。Randers等人（2010）使用四种不同的运动捕捉系统（基于视频的时间 - 运动分析系统 - VTM，半自动多摄像机系统 - MCS，以及两种商业可用的GPS系统：5 Hz GPS和1 Hz GPS）比较了20名足球运动员在一场比赛中的活动。尽管这四种系统都能够跟踪球员，但在比赛中覆盖的总距离方面，GPS（5 Hz GPS为，1 Hz GPS为）与其他两个系统（MCS为，VTM为）之间观察到显著差异。高强度跑步覆盖的距离在5 Hz GPS（）和MCS（）之间以及在1 Hz GPS（）和MCS（）以及VTM（）之间存在显著差异。冲刺覆盖的距离在1 Hz GPS（）和VTM（）以及MCS（）之间存在显著差异，而5 Hz GPS（）与VTM和MCS没有显著差异。Randers等人（2010）得出结论，在确定绝对覆盖距离方面存在较大的系统间差异，这意味着使用不同比赛分析系统进行结果比较时应该谨慎。在另一项研究中，Waldron等人（2011）研究了5 Hz GPS和计时门（Brower Timing Systems，Draper，UT）在测量橄榄球运动员冲刺速度和距离方面的有效性和可靠性，以及通过GPS - 加速度计集成记录的适当加速度的可靠性。有效性结果表明，GPS测量系统地低估了距离和计时门速度（变异系数在4.81%到9.81%之间）。当比较两次测试之间的GPS测量值时，观察到所有距离和速度变量的高可靠性（变异系数在1.62%到2.3%之间）。然而，计时门比等效的GPS测量更可靠（变异系数在1%到1.54%之间）。

　　最后，加速度测量（通过GPS - 加速度计集成）不太可靠（变异系数在4.69%到14.12%之间，当比较两次测试之间的峰值加速度和频率时）。Waldron等人（2011）得出结论，计时门和GPS是评估速度和距离的可靠系统，尽管GPS的有效性仍然值得怀疑。在加速度测量中发现的误差（通过GPS - 加速度计集成）表明了该设备在检测性能变化方面的局限性。一种提高GPS准确性的方法可能是通过融合GPS、IMU、摄像机和数字地图的数据（Baranski & Strumillo, 2012）。Baranski和Strumillo（2012）在行人导航中这样做了，对于90%的导航时间，该算法能够以小于2 m的误差估计行人位置，而仅基于GPS的导航误差为6.5 m（Baranski & Strumillo, 2012）。

　　此外，如前所述，IMU可以记录长期数据，然后可以提取离散特征，或者在循环活动（例如，划船、骑自行车、游泳、跑步）的情况下，可以进行时间序列分析，例如循环间变异性调查。例如在游泳中，Dadashi, Millet, 和Aminian（2016）分析了在400 m自由泳中超过5,000个循环的运动和协调模式。尽管IMU已经经历了快速发展，但基于节段旋转计算的高级别指标（如关节或节段角度）的计算仍然容易出错，需要逐步进行（例如，IMU在身体上的定位、校准、数据收集和后处理）以获得准确和有效的指标。根据Teuf, Miezal, Taetz, Fröhlich, 和Bleser（2018）在步行任务和Ahmadi, Rowlands, 和James（2013）在网球发球任务中的研究，将IMU放置在刚性簇上而不是直接放在参与者的皮肤上应该提供更准确的结果。实际上，由于肢体运动导致的簇的3D误差表面运动的这种估计应该从计算的角度中减去，以最小化由于标记运动导致的误差（Ahmadi等人，2013）。

　　然而，校准的准确性仍然取决于运动员执行校准程序的准确性（Seel等人，2014）。因此，Seel等人（2014）提出了一种方法来应对IMU和肢体可能的错位，在校准过程中使用任意膝盖运动。通过10秒的任意膝盖运动，这些作者计算了取决于IMU在肢体上初始位置的单位长度方向向量。然后，Seel等人（2014）整合了关节轴在屈伸运动期间的角速度差异，这产生了一个高度准确但缓慢漂移的关节角度。这个角度在传感器融合中与一个有噪声但无漂移的关节角度估计相结合，该估计是从测量的加速度计算出来的（Seel等人，2014）。与视动Vicon系统相比，他们的模型在六个步态试验中为膝关节估计提供了有效的结果，平均RMSE值为在校准问题之后，另一个问题与陀螺仪测量随着时间的渐进漂移有关。实际上，对于任何类型的测量（即，静态、简单2D或复杂3D记录），由于角速度测量中的噪声或小偏移，漂移会积累。

　　此外，尽管IMU方向可以通过陀螺仪记录的时间积分来计算，但这个过程揭示了低频陀螺仪偏差漂移（Sabatini, 2011）。为了限制这种现象，IMU的倾斜度可以从加速度计估计，加速度计是无漂移的，并将其测量与重力向量结合。从那里，两个传感器记录的结合可能成为纠正陀螺仪漂移和更好估计3D传感器位置的可行解决方案。Zhou和Hu（2013）使用了一个卡尔曼滤波器，它比较从加速度计和陀螺仪测量的倾斜度，它们之间的差异然后用于纠正估计的方向。他们还整合了节段长度以更好估计每个节段的位移（Zhou和Hu，2013；Zhou, Stone, Hu, & Harris, 2013）。在游泳中，Seifert, Komar, Hérault, 和Chollet（2014），以及Dadashi等人（2012）分别观察到了这种角度计算和速度评估的漂移。Seifert, Komar, Hérault, 和Chollet（2014）提出了一种对肘部角度时间序列上的这种（伪线性）漂移进行简单纠正的方法，通过包裹信号的峰值和谷值。这个程序给出了峰值和谷值形状保持的样条曲线（在某些情况下是直线，当漂移是完全线性的时候），这些被认为是记录的最大值和最小值。这个程序不能提供绝对角度值，但只提供在 - 1和1之间归一化的相对值，并且允许比较时间序列的循环（Seifert, Komar, Hérault, 和Chollet, 2014）。

　　IMU的有效性可以通过斯皮尔曼等级相关（或斯皮尔曼）来评估，以验证从IMU获得的值与金标准系统（如视动多摄像机系统）之间的统计依赖性。然而，这种计算忽略了测量偏差，测量偏差通过布兰德和奥特曼分析（1986）进行评估，以通过比较系统之间的一致性更好地描述IMU的有效性。一致性界限（LoA）计算为平均偏差（布兰德 & 奥特曼，1986）。Taylor, Miller, 和Kaufman（2017）在一个轮子上进行了动态验证测试，以检查IMU的有效性，发现IMU在较低速度下比金标准更准确。Cutti, Giovanardi, Rocchi, 和Davalli（2013）发现了类似的结果，并强调IMU的测量误差通常随着速度增加而增加。

　　假设陀螺仪容易漂移，可靠性通过计算数据随时间的内部一致性来估计（Dadashi等人，2012）。因此，倾向于使用归一化成对变异性指数（nPVI）（Sandnes & Jian, 2013），因为它评估了循环时间序列中的空间变异性（例如，对正弦波信号的每个周期进行计算）：其中是两个比较系统执行的第次测量，N是相应材料获取的数据总量。可靠性也可以量化为视动信号和IMU信号上局部最大值出现的时间差。例如，Zanone和Kelso（1992）建议在两个信号是周期性或伪周期性时计算它们之间的离散相对相位：，离散相对相位以度为单位计算；对应于IMU信号的移动峰值，对应于视动信号的移动峰值，T是视动信号的周期。当计算离散相对相位时，可以量化IMU信号相对于金标准的任何暂时或反复的时间偏移。最后，数据准确性可以通过计算IMU和视动多摄像机系统获得的整个时间序列之间的均方根误差（RMSE）来评估（Rein, 2013）：

　　其中n是在系统之间同时处比较的数据对总数。RMSE值接近零表明IMU记录的数据相对于视动多摄像机系统获得的值的离散程度有限。Zhou和Hu（2013）测试了上肢运动的不同运动速度，发现速度对RMSE值（视动Qualisys多摄像机系统和Xsens套装的IMU之间的绝对平均误差约为）没有显著影响。Nüesch, Roos, Pagenstert, 和Mündermann（2017）在步行测试中观察到IMU膝关节角度测量和金标准之间的RMSE值在到之间。在游泳中，de Magalhães等人（2013, 2015）研究了五次自由泳划水时的肩部运动学，测量了立体摄影测量系统和IMU之间的角度差异。上臂和胸腔之间的角度显示RMSE值在到之间（平均值为）。在同一任务中，在近20个划水周期中进行，Fantozzi等人（2014）报告了两个系统的平均RMSE值为，最大差异出现在肘部旋前 - 旋后和屈伸（分别为和）。根据以前的研究，或更小的误差被认为是可接受的，因为这样的误差可能太小，在数据解释过程中不需要明确考虑（Cuesta - Vargas, Galán - Mercant, & Williams, 2013；McGinley, Baker, Wolfe, & Morris, 2013）。误差在到之间也可能被认为是合理的，但可能需要在数据解释中考虑。最后，Cuesta - Vargas等人（2013）建议误差大于应该引起关注，并且可能足够大，足以误导解释。这些建议与Poitras等人（2013）最近的系统综述一致，他们回顾了比较IMU和运动捕捉系统用于身体关节角度估计的研究。

　　运动表现意味着理解个体能力如何与环境机会相匹配以及它们如何在比赛或竞赛的连续任务中动态相互作用。因此，感兴趣的变量不能忽视表现展开的环境。更确切地说，数据来源不能仅仅位于执行者身上，而需要捕捉运动员如何调整和实现表现环境的任务目标。可供性的作用以及对其的感知协调和行动准备似乎至关重要。这是生态动力学框架所关注的。特别是，生态动力学理论方法从以下理解出发：（i）表现从执行者 - 环境系统中产生；（ii）为了理解个体的表现，分析其环境提供的行为（即，可供性）是必要的；（iii）表现（作为自组织的结果）在相互作用的约束下产生（Araújo & Davids, 2018; Araújo等人，2020; Button等人，2020）。这种方法意味着生态生理变量（Araújo等人，2020）是捕捉智能行为的最佳起点（见第1章）。这些是表达环境与执行者适应之间契合度的变量。如前所述，环境属性可以直接告知一个人能做什么和不能做什么，这就是为什么代表性评估任务如此重要（Araújo & Davids, 2015; Davids等人，2012）。研究人员和从业者面临的一个重要挑战是在体育中连续、突发的执行者 - 环境相互作用期间捕捉基于感知 - 行动耦合的生态生理变量。接下来我们介绍体育科学研究中在足球、橄榄球、游泳和攀岩方面的例子。

　　Carrilho等人（2020）利用2018年俄罗斯世界杯一场比赛的时空数据，捕捉了团队协同特性，在聚类阶段分析中分析了生态生理变量“球员 - 球 - 球门角度”。相对相位分析（RPA）在团队体育中被用于测量同步（例如，Travassos, Araújo, Duarte, & McGarry, 2012）。RPA基于两个相位之间振荡的差异，作为它们相对相位角的度量，由它们的角频率（ω）和初始相位（）定义。在一个时间序列中的两个振荡器可以以同相模式同步，如果它们的角度差异接近，或者以反相模式同步，如果角度接近。基于这个想法，聚类阶段分析（CPA）也测量同步，但它基于一组元素的振荡运动之间的关系，使用Kuramoto序参数（Duarte等人，2013）。因此，与RPA不同，CPA测量一组元素内振荡相位之间的同步。在Carrilho等人（2020）的研究中，他们在CPA中分析了球员 - 球 - 球门角度（PBGAs），以直接测量球员 - 环境关系并捕捉团队协同行为的特性（Araújo & Davids, 2016）。球、球门和球员被确定为足球比赛的关键生态变量，因为它们告知和约束球员的行为。因此，通过使用PBGA，他们捕捉了球员和表现环境之间的联系，为CPA提供了生态解释价值。从CPA获得的同步测量结果是球员 - 球 - 球门角度（PBGA）变化的直接结果，它不断捕捉球员在球场上相对于球门和球的位移。位置数据由葡萄牙足球联合会（FPF）提供，并通过TRACAB光学跟踪系统（ChyronHego）获得（见Linke, Link, & Lames, 2020）。数据集包含每个球员（）和球（）的位置数据，以25 Hz的频率采集，空间分辨率为0.01 m。对于CPA测量，每个集群（团队）由球场上相应的球员组成。对于每个球员，球员 - 球 - 球门角度在到之间变化，并在每个时间帧计算，以球为顶点，使用每个球员、球和球门的平面坐标，如公式（3.1）所示。球员 - 球 - 球门角度是在球门受到攻击时计算的。

　　结果表明，主队的聚类阶段值（同步性）相对于客队有所增加，并且从有球到无球的角色变化会增加同步性。球员 - 团队相对相位、球员 - 球 - 球门角度相对频率以及团队配置表明，同步性的变化可能预示着关键的比赛表现变化（控球权变化、进球等）。球员 - 球 - 球门角度（PBGA）一致地捕捉到了团队协同行为的特性，使用同步性测量。此外，聚类阶段分析（CPA）结合球员 - 球 - 球门角度（PBGA），可能在比赛结果发生变化之前就捕捉到这些变化，体现在同步性值的动态变化中。这项研究表明，同步性的变化显示了球队表现平衡的变化，这可能与比赛结果的变化有关。简而言之，这个生态生理变量（球员 - 球 - 球门角度，PBGA）能够直接测量球员与环境之间的联系，因为这些测量值直接受到球员相对于关键生态变量的位置的影响。

　　Passos等人（2008, 2009）确定了一个生态生理变量，该变量描述了橄榄球中攻方 - 守方二人组的时空关系。攻方球员需要拿着球从距离达阵线 m的位置跑过守方球员。生态生理变量的值是根据守方 - 攻方向量与一条平行于达阵线的假想水平线之间的夹角计算的，该夹角的原点位于守方球员的位置。这个生态生理变量在攻方球员到达守方球员位置之前显示接近的角度，在攻方球员成功越过守方球员之后显示接近的角度，并且当攻方球员越过守方球员时恰好出现零交叉点（Passos等人，2009）。根据这一实证证据，我们对这个攻方 - 守方 - 得分线系统动力学进行了建模（Araújo, Diniz, Passos, & Davids, 2014）。重要的是，尽管双方球员可能采取的行为轨迹可能有很大的变化，但这个系统被吸引到三个状态之一：守方的擒抱、守方擒抱对攻方有利以及攻方的达阵。对这个橄榄球系统进行建模的势函数能够描述其动力学，因为球员和环境由于生态生理变量而被捕捉。

　　在游泳生物力学中，游泳者的运动学通常通过3D多摄像机系统进行评估（Bernardina等人，2016, 2017; de Jesus等人，2015; Figueiredo, Machado, Vilas - Boas, & Fernandes, 2011; Gourgoulis等人，2008），以便确定划水周期的关键点（例如，手入水、抓水点、最大向前坐标、最大向后坐标、手出水；Aujouannet, Bonifazi, Hintzy, Vuillerme, & Rouard, 2016），这使我们能够定义划水阶段（例如，向外、向内；推进和非推进阶段；Chollet, Chalies, & Chatard, 2000; Ribeiro等人，2017）。通常，这些测量是在以自我为中心的参考系中进行的。因此，手的推进力通常是相对于肩部位置并参照质心来表示的。这并不意味着以自我为中心的参考系没有意义，但它没有捕捉到游泳者与水生环境的相互作用，例如游泳池的水面或游泳轴（Guignard等人，2017a）。根据生态动力学框架，生态生理变量，如躯干与水位之间的角度，或手臂与重力方向之间的角度，将表明游泳者何时处于流线型位置以及水动力是如何扰的（例如，由于摇摆、俯仰和滚动身体运动），例如在呼吸或逆流游泳时（Guignard等人，2017a, 2020）。为此，Guignard等人（2017a, 2020）使用惯性测量单元（IMU）评估近端（上臂与手臂之间）和远端（手与手臂之间）的节段间角度和协调。

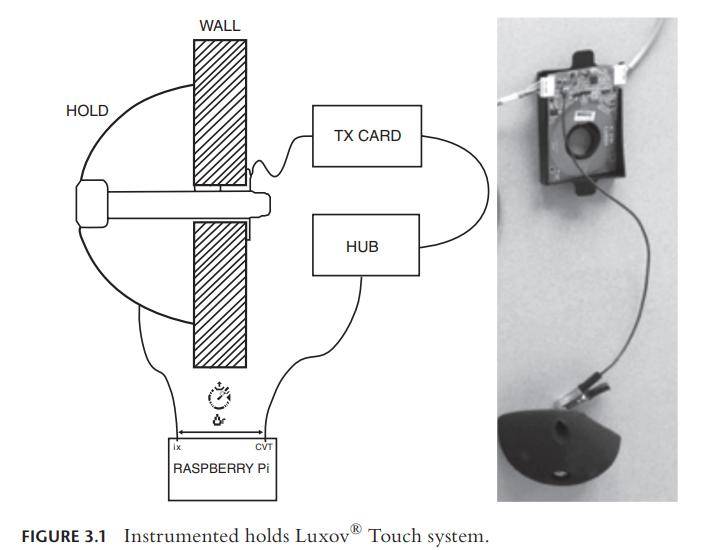
　　虽然攀岩的本质与户外有关，但运动攀岩越来越受欢迎，并且在攀岩馆（即人工攀岩墙）中进行，在那里路线设置者可以设计非常不同的攀岩问题，提供丰富的可供性景观，这将使获得的技能能够转移到户外。为了评估路线设计对表现的影响，可以测量几个生态生理变量，如运动时间与静止时间的比率（Orth, Kerr, Davids, & Seifert, 2017; Orth, Davids, Chow, & Brymer, & Seifert, 2018a; Seifert等人，2018），并且最近Seifert, Hacques, Rivet, and Legreneur（2018）提出了一种新设备（Luxov® Touch, Luxov, Arnas, France, 来评估在每个支点上的接触时间，以便研究支点逐个的流畅性。接触时间是一个生态生理变量，它可以确定哪个支点需要更长的静止时间，这通常反映了“难点”（即路线中最困难的部分）。它为路线设置者和从业者提供信息，以了解路线设计如何影响攀岩的流畅性。流畅性的缺乏也可以通过空间指标来研究，如反映攀岩路径复杂性的几何熵指数（Figure 3.1）（Orth, Davids, & Seifert, 2018b; Sibella, Frosio, Schena, & Borghese, 2017; Watts, España - Romero, Ostrowski, & Jensen, 2020）或身移的平滑度（对应于加速度导数的急动运动；Seifert, Orth等人，2014）。最后，Seifert, Boulanger, Orth, and Davids（2015），以及Orth和同事（2018b）研究了一个生态生理变量，该变量捕捉身体相对于墙壁的滚动如何解释攀岩流畅性的变化。为此，路线设置者设计了三条不同的路线，通过操纵支点的方向和可用的抓握边缘数量。设计了一条水平边缘路线，当观察到躯干面向墙壁时，允许水平抓握支点。设计了一条垂直边缘路线，允许垂直抓握支点，对于有经验的攀岩者，通常会出现更具挑战性的躯干侧面靠墙的情况。最后，设计了一条双边缘路线，允许水平和垂直抓握支点。由于只有垂直边缘支点的路线对新手攀岩者来说非常具有挑战性，双边缘路线将允许安全和功能性的探索，因为攀岩者既可以利用他们的稳定模式（即水平抓握支点模式和躯干面向墙壁）与流畅运动相关联，又可以探索新的行为（即垂直抓握支点和躯干侧面靠墙）与不太流畅的运动相关联（Seifert等人，2015）。

　　本章解释了结合准确可靠的时间 - 运动运动学分析的代表性，以便对运动表现提供更全面的生态动力学理解。然后，它根据运动类型（个人和集体）讨论了数据收集的设计方法，定义了任务、程序和相关技术。它强调了通过围绕低级别运动学表现指标和相关生理见解进行讨论来描述运动表现的设备和变量。它还研究了将这些直接表现指标组合成复合指标的情况，并在设计任务、选择相关技术、设置数据收集和计算指标时提出了谨慎的要求。遵循生态动力学理论框架，我们提出生态生理变量作为捕捉运动表现相关问题的一种手段，因为表现是在执行者 - 环境系统层面定义的。决策通常涉及在有效性、准确性、可靠性以及（i）设置、收集、分析和为从业者提供反馈的时间约束，以及（ii）任务和执行任务的环境的性质之间进行妥协，这对设计代表性提出了质疑。